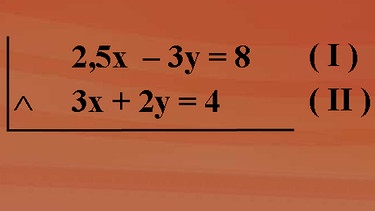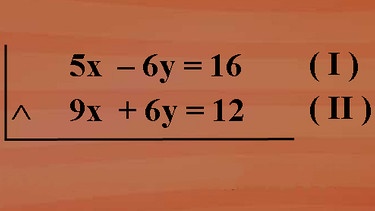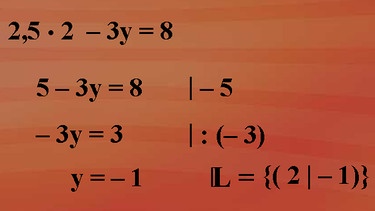Grundkurs Mathematik (5) 5.5. Das Additionsverfahren
In Fällen, wo Einsetzverfahren und Gleichsetzverfahren viel zu umständlich wären, hat die Mathematik noch ein "Schmankerl" zu bieten: die Königsdisziplin, das Additionsverfahren. Heinz Gascha führt es vor.
Die Gleichungssysteme sind nicht immer so einfach wie unser Beispiel. Oftmals sind viele Rechenschritte nötig, um entweder das Einsetzverfahren oder das Gleichsetzverfahren anwenden zu können.
Rechenbeispiel - klicken Sie bitte auf die Lupe
Nehmen wir mal das Gleichungssystem 2,5x minus 3y ist 8 für Gleichung I und 3x plus 2y ist 4 für Gleichung II in der Grundmenge G gleich Q kreuz Q. Sowohl das Einsetzverfahren als auch das Gleichsetzverfahren führen hier zu einer Menge Rechnerei.
Die Erkenntnis aus dem Video wollen wir für unser Gleichungssystem anwenden:
Lösungsweg mit dem Additionsverfahren
Rechenbeispiel - klicken Sie bitte auf die Lupe
Multiplizieren wir unsere erste Gleichung mit 2 und die zweite Gleichung mit 3, so erhalten wir 2 Gleichungen, bei denen die Koeffizienten der Variablen y entgegengesetzte Zahlen sind, nämlich plus 6 und minus 6.
Bei der Addition der beiden Gleichungen entfällt somit die Gleichungsvariable y, was ja das Ziel unserer Verfahren ist, und wir haben mit 14x ist 28 eine Gleichung mit einer Variablen. Mit 14 geteilt haben wir schon die Lösung mit x gleich 2.
Das Lösungspaar - klicken Sie bitte auf die Lupe
Ab hier geht es wie bei den anderen Verfahren weiter.
Wir setzen x in eine der beiden Ausgangsgleichungen ein, hier in Gleichung I, und bekommen 2,5 mal 2 für x, minus 3y ist 8. Nach y aufgelöst über ein, zwei Umformungen y gleich minus 1. Und somit die Lösungsmenge mit dem Lösungspaar 2 und minus 1.
Die Königsdisziplin
Haben Sie gesehen, wie einfach auch dieses schwierige Gleichungssystem mit der neuen Methode zu lösen war? Man nennt dieses dritte Verfahren, die Königsdisziplin unter den Lösungsmethoden für lineare Gleichungssysteme, das Additionsverfahren.
Das Additionsverfahren:
Durch Multiplikation jeder der Gleichungen mit einer geeigneten Zahl erreicht man, dass die Koeffizienten einer der Gleichungsvariablen in beiden Gleichungen entgegen gesetzte Zahlen sind. Bei der Addition der beiden Gleichungen wird somit eine Gleichungsvariable eliminiert, einfacher gesagt sie verschwindet oder entfällt.