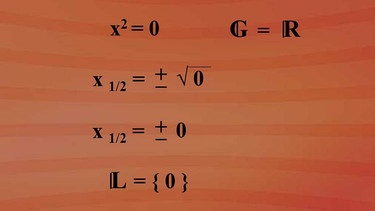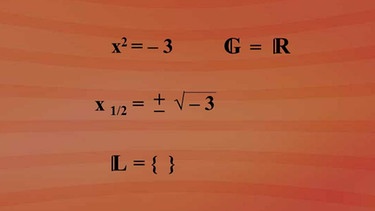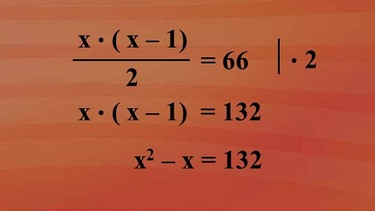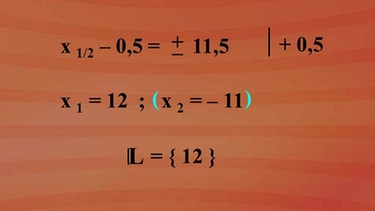In dem vorher gezeigten Beispiel mit dem Mauerbau haben wir eine Anwendung für das Radizieren gefunden. Es ist ein Hilfsmittel zum Lösen von quadratischen Gleichungen. Besitzt nämlich eine Gleichung mindestens eine Lösungsvariabel, in unserem Fall war dies das kleine a, als Quadrat, so spricht man von einer quadratischen Gleichung. Und unser Fall war zudem noch ein Sonderfall, da die Gleichung nur aus dem Quadrat der Variablen und einem konstanten Wert bestand. Gleichungen dieser Art nennt man rein quadratische Gleichungen.

Beispiele mit der Gleichungsvariablen x

x hoch zwei ist 49. Diese Gleichung hat in der Grundmenge R zwei Lösungselemente.

Man schreibt x eins strich zwei für die beiden Möglichkeiten ist gleich plus oder minus Wurzel aus 49.

Und die Wurzel aus 49 ist sieben. Die beiden Lösungselemente werden in die Lösungsmenge aufgenommen.

Haben rein quadratische Gleichungen immer zwei Lösungen? Dieser Sache gehen wir mal auf den Grund. Wie sieht es bei der Gleichung "x hoch zwei gleich Null" aus? Nach dem gleichen Verfahren erhalten wir nur ein Lösungselement.

Für die Gleichung "x hoch zwei gleich minus drei" erhalten wir kein Lösungselement, da es keine Zahl gibt, die mit sich selbst multipliziert einen negativen Wert ergibt.

Gemischt quadratische Gleichung

Stellen Sie sich vor: Sie waren auf einer Party und haben mitgezählt, wie oft angestoßen wurde, als zur Begrüßung jeder mit jedem Besucher einmal die Sektgläser erklingen ließ. Zu Hause werden Sie gefragt, wie viele Personen auf der Party waren. Sie haben sie nicht gezählt, aber insgesamt wurde zur Begrüßung 66 mal angestoßen. Wie viele Gäste waren auf der Party?

Beispiel für eine gemischt quadratische Gleichung - klicken Sie bitte auf die Lupe.

Wenn jeder mit jedem anstößt, müssen x mal x minus eins Begrüßungen beidseitig stattgefunden haben. Da es nur einmal klingt, muss dieses Produkt noch durch zwei dividiert werden und wir erhalten die Gleichung x mal x-1 in Klammern geteilt durch zwei ist 66. Mit zwei multipliziert ergibt sich x mal x-1 in Klammern gleich 132. Multiplizieren wir die Klammer aus haben wir auf der linken Seite x2 minus x.

Es handelt sich also um keine rein quadratische Gleichung mehr, da die Gleichungsvariable x sowohl mit der Potenz zwei als auch mit der Potenz eins auftritt. Man nennt Gleichungen dieser Art gemischt quadratische Gleichungen. Und gelöst werden sie durch einen kleinen Trick.

Lösung einer gemischt quadratischen Gleichung

Lösung einer gemischt quadratischen Gleichung: klicken Sie bitte auf die Lupe.

Wir ergänzen den Linksterm der Gleichung so, dass sich ein Binom ergibt. Dies geschieht mit plus 0,5 zum Quadrat. Damit die Gleichung wahr bleibt, muss die Rechenoperation auch am Rechtsterm der Gleichung ausgeführt werden. Man nennt dieses Addieren mit einer geeigneten Zahl quadratische Ergänzung. Jetzt wird auf der linken Seite der Gleichung die 2. Binomische Formel angewendet und auf der rechten Seite addiert. Und ab hier geht es analog zur rein quadratischen Gleichung weiter. Auf beiden Seiten radiziert erhalten wir x eins Strich zwei für die beiden Lösungsmöglichkeiten, minus 0,5 ist gleich plus oder minus die Wurzel aus 132,25. Und die Wurzel aus 132,25 ist laut Taschenrechner 11,5.

Auf beiden Seiten 0,5 addiert, kommen wir zu den beiden Lösungen x eins gleich 12 und x zwei gleich minus 11. Die zweite Lösung kann hier ausgeklammert werden, da die Grundmenge für die anwesenden Personen sicher die Menge der natürlichen Zahlen sein muss. Ergebnis: Es waren zwölf Personen auf der Party anwesend.