Wie im Film zu sehen war, haben die Schüler von Pythagoras zuerst quadriert, um die Quadratflächen zu ermitteln. Danach versuchte der Schüler Hippasus das Umgekehrte. Und diese Umkehrung des Quadrierens wird für nicht negative Zahlen als Wurzelziehen oder nach dem lateinischen Wort radix, was Wurzel bedeutet, als Radizieren bezeichnet. Als Symbol verwendet man ein stilisiertes r, von radix.

Das Wurzelzeichen

Die ersten modernen Wurzelzeichen findet man in der Literatur aus dem 15. Jahrhundert. Das r wurde nach und nach etwas verändert, bis es die heutige Form des Mathematikers Michael Stifel bekam.

Quadratwurzel aus zwei

Quadratwurzel aus zwei - klicken Sie bitte auf die Lupe

Der genaue Wert, der mit sich selbst multipliziert zwei ergibt, ist also die Quadratwurzel aus zwei. In nebenstehender Grafik ist der Wert auf der Zahlengerade eingetragen. Statt den Näherungswert 1,4142 schreiben wir den ganzen Wert Wurzel aus zwei.

Ein neuer Zahlenbereich

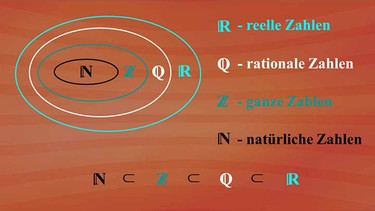
Nach diesem Schema gibt es auch die Quadratwurzel aus jeder beliebigen Zahl. Manchmal eindeutig, wie bei der Quadratwurzel aus vier, denn zwei mal zwei gibt vier, oder nicht genau bestimmbar, wie die Quadratwurzel aus fünf, deren Ergebnis zwischen zwei und drei liegt. Sollen alle Lücken auf der Zahlengeraden geschlossen werden, so ist ein neuer Zahlenbereich erforderlich, der die wirklich vorhandenen Zahlen darstellt. Und dieser neue Zahlenbereich ist die Menge R der reellen Zahlen.

Er beinhaltet die Menge der rationalen Zahlen, die wiederum die Menge der ganzen Zahlen und die Menge der natürlichen Zahlen beinhalten. N ist eine Teilmenge von Z, Z wiederum eine Teilmenge von Q, und Q eine Teilmenge aus den reellen Zahlen R.

Die reellen Zahlen beinhalten neben den rationalen Zahlen unendlich lange nicht periodische Dezimalbrüche.