8. Die reellen Zahlen 8.3. Mit Wurzeln rechnen
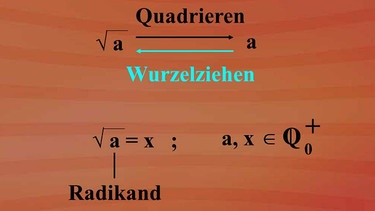
Welcher Zusammenhang besteht zwischen Quadrieren und Wurzelziehen? Ganz einfach: Es ist die jeweilige Umkehrung. An einfachen Beispielen wird dieser Zusammenhang deutlich.

Das Wurzelziehen ist die Umkehrung des Quadrierens. Die Quadratwurzel aus a ist die positive Zahl x, die beim Quadrieren a ergibt. Man schreibt dafür Quadratwurzel aus a ist x ,für a und x Element aus Q Null plus. Der Term unter der Wurzel wird als Radikand bezeichnet.
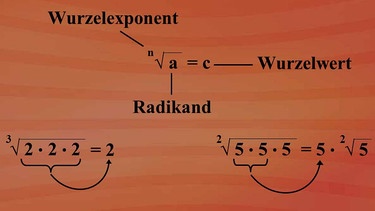
Der Wurzelexponent
Allgemein ist das Radizieren die Umkehrung vom Potenzieren. Es wird aber nicht nur mit der Hochzahl zwei potenziert, sondern auch mit drei, vier und so weiter, also bis n. Der Wurzelexponent n gibt an, wie oft der Faktor a unter dem Wurzelzeichen auftreten muss, damit er einmal vor das Wurzelzeichen gezogen werden darf.
Beispiele
Das Ergebnis liefert uns den Wurzelwert. Beispiele dazu:
Die dritte Wurzel aus zwei mal zwei mal zwei: Da der Faktor zwei dreimal unter der Wurzel steht, darf er wegen der dritten Wurzel einmal vor die Wurzel gezogen werden. Der Wurzelwert beträgt zwei. Oder die Quadratwurzel aus fünf mal fünf mal fünf. Wegen des Wurzelexponenten zwei können jeweils zwei Faktoren zusammengefasst und einmal vor die Wurzel geschrieben werden. Wir erhalten fünf mal Quadratwurzel aus fünf.
Die Quadratwurzel aus fünf könnten wir über Interpolation bestimmen oder in unserem modernen Zeitalter mit dem Taschenrechner berechnen.