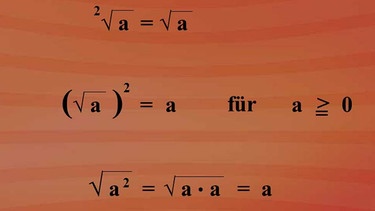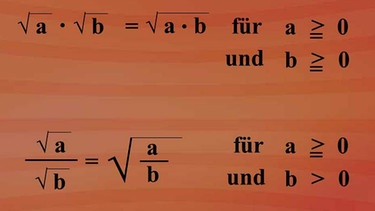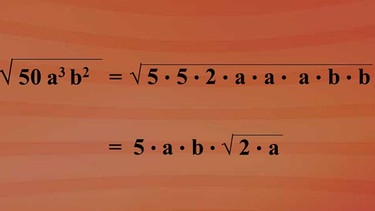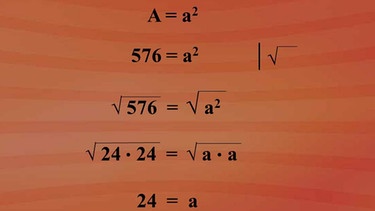8. Die reellen Zahlen 8.4. Wurzelgesetze
Wer eine Steinmauer bauen will, braucht Steine. Um zu wissen, wie viele Steine er braucht, muss er mit Wurzeln rechnen - und Regeln für das Rechnen mit Wurzeln kennen. Diese Regeln werden hier vorgestellt.
Generell gilt: Die Quadratwurzel kann auch ohne Wurzelexponent angegeben werden. Zweite Wurzel aus a hat die gleiche Bedeutung wie Wurzel aus a. Man muss auch nicht immer Quadratwurzel sagen, denn unter der Wurzel versteht man automatisch die Quadratwurzel. Nur alle anderen Wurzeln müssen genau bezeichnet werden.
Regeln für das Rechnen mit Wurzeln
In der Praxis beschafft man sich von Quadratwurzeln, die keine rationalen Zahlen sind, Näherungswerte und rechnet mit diesen Werten. Möchte man aber mit genauen Werten rechnen, muss man die Wurzelschreibweise beibehalten und die Rechenausdrücke nach bestimmten Regeln, den sogenannten Wurzelgesetzen, umformen.
Zusammenstellung der wichtigen Gesetzmäßigkeiten
Eine Quadratwurzel quadriert, ergibt als Ergebnis den Radikand. Zwei mal ein gleicher Faktor unter der Wurzel gibt einmal den Faktor außerhalb der Wurzel. Bei der Multiplikation von Wurzeln dürfen die Radikanden unter eine Wurzel zusammengefasst werden.
Gleiches gilt auch für die Division Wurzel a durch Wurzel b ist Wurzel aus a durch b. Hierbei darf b nicht gleich Null sein, da eine Division durch Null nicht erlaubt ist.
Rechnen mit Variablen
Arbeitet man nicht nur mit Zahlen, sondern auch mit Variablen, so kann man oftmals nur Termteile radizieren. Ein Beispiel:
Wurzel aus 50 a hoch drei b hoch zwei. Ein Faktor muss zwei mal unter der Wurzel auftreten, damit man ihn einmal vor die Wurzel ziehen kann. Dazu faktorisieren wir den Radikand weit möglichst und erhalten Wurzel aus fünf mal fünf mal zwei für 50, a mal a mal a für a hoch drei und b mal b für b hoch zwei. Je zwei mal treten die fünf, die Variablen a und b auf. Somit kann man sowohl die fünf als auch die Variablen a und b je einmal vor das Wurzelzeichen ziehen und es bleibt unter der Wurzel der Term zwei mal a stehen.
Da nicht alles radiziert wurde, nennt man diese Art des Wurzelziehens "teilweises Radizieren".
Bitte merken!
Es darf nur aus Produkten und Quotienten radiziert werden. Ist der Radikand eine Summe oder eine Differenz, so muss man den Summenwert beziehungsweise den Differenzwert bilden bevor radiziert werden kann.
Wie kam der Verkäufer im Film auf das Ergebnis? Die Fläche eines Quadrates beträgt A ist a hoch zwei. Die Flächenmaßzahl ist 576. Um von a hoch zwei auf a zu kommen, müssen wir die Wurzel ziehen. Damit die Gleichung wahr bleibt, muss man es auf beiden Seiten tun. Wir erhalten: Wurzel aus 576 ist Wurzel aus a hoch zwei. Beide Radikanden faktorisiert ergeben Wurzel aus 24 mal 24 ist gleich Wurzel aus a mal a. Und jetzt das bereits Gelernte angewandt: Zweimal der gleiche Faktor unter der Wurzel gibt einmal den Faktor außerhalb der Wurzel und schon haben wir das Ergebnis des Verkäufers.