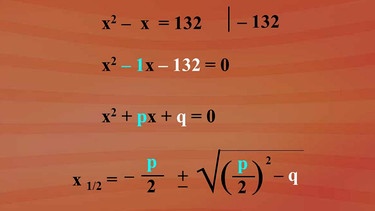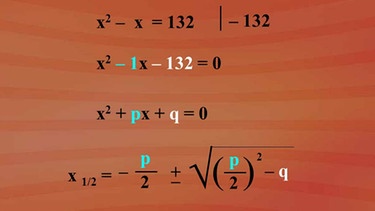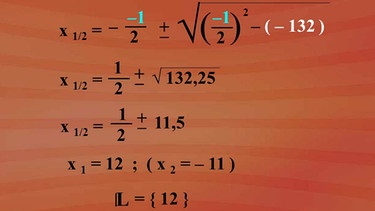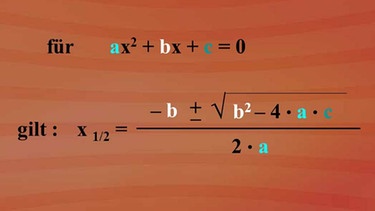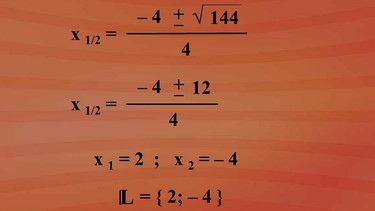Um eine quadratische Gleichung, die in der Form "x hoch zwei plus p mal x plus q gleich Null" gegeben ist, zu lösen, kann man die Formel x eins strich zwei ist gleich minus p halbe plus oder minus Wurzel aus p halbe in Klammern zum Quadrat minus q verwenden.

Umformung der Ausgangsgleichung

Um die Formel anwenden zu dürfen, muss die Ausgangsgleichung in der richtigen Form angegeben sein. Deshalb wird die Ausgangsgleichung dementsprechend umgeformt:

Die Gleichung "x hoch zwei minus x ist gleich 132" wird als Gleichung vor der durchgeführten quadratischen Ergänzung übernommen. Um die Form "x hoch zwei plus p mal x plus q gleich Null" zu erreichen, subtrahiert man beidseitig 132 und erhält x hoch zwei minus x oder minus 1x geschrieben minus 132 gleich Null. Dem p ist minus eins und dem q minus 132 zugeordnet.

Einsetzen in die Lösungsformel

Diese Zahlenwerte werden für die Belegung der Formvariablen in der Lösungsformel eingesetzt. Wir erhalten "x eins Strich zwei gleich minus, minus eins für p eingesetzt, halbe plus oder minus Wurzel aus minus eins durch zwei in Klammern zum Quadrat minus, minus 132 für q eingesetzt.

Der Lösungsweg: Klciken Sie bitte auf die Lupe.

x eins Strich zwei ist minus und minus gibt plus eins durch zwei plus oder minus Wurzel aus minus einhalb zum Quadrat gibt 0,25 und mit 132 addiert - da wieder minus und minus plus ergibt - 132,25. Und die Wurzel aus 132,25 ist 11,5. Auch hier ergeben sich die Lösungen x eins gleich 12 und x zwei gleich minus 11. In der Grundmenge N das Lösungselement zwölf.

Voraussetzung für die Lösungsformel

Die hier benützte Lösungsformel kann aber nur angewendet werden, wenn die quadratische Gleichung die Form eins mal x hoch zwei plus und so weiter aufweist. In vielen Schulbüchern wird eine zweite Lösungsformel verwendet. Sie wird angewandt, wenn die quadratische Gleichung die allgemeine Form "a mal x hoch zwei plus b mal x plus c ist gleich Null" hat. Der Vorteil ist, dass man die Gleichung nicht durch den Koeffizienten a von x hoch zwei dividieren muss, ehe man die Formel anwendet.

Die Lösungen dazu lauten:

x eins Strich zwei ist gleich minus b plus minus Wurzel aus b hoch zwei minus vier mal a mal c und das alles durch zwei mal a.

Übungsbeispiel

Gegeben ist eine beliebige quadratische Gleichung mit zwei x hoch zwei plus vier x minus 16 ist Null in der Grundmenge R. Die Formvariablen a, b, c für die Formel werden zugeordnet und können direkt eingesetzt werden.

Überall wo ein b steht übernehmen wir die Vier, für a die Zwei und für c minus 16.

Den weiteren Lösungsweg sehen Sie in nebenstehender Grafik - bitte klicken Sie auf die Lupe. Der Radikand ergibt 144 und radiziert zwölf. Es ergeben sich die Lösungen x eins gleich zwei und x zwei gleich minus vier. Da die Grundmenge R gewählt wurde, können beide Lösungen in die Lösungsmenge übernommen werden.