Wenn Sie die Mathematik als Spiel betrachten, wie zum Beispiel das Zahlenkartenspiel SkipBo oder das alte Schwarze-Peter-Spiel, fällt alles viel leichter. Lassen wir unser Spiel beginnen:

Schnittmenge

Wenn Sie genau beobachtet haben, war erkennbar, dass die beiden Kartenspieler Karten mit gleichen Bildern besaßen, nämlich diese, welche in die Mitte zusammengelegt wurden.

Nehmen wir jetzt einmal an, die Karten des ersten Spielers entsprechen einer Menge M₁, die des zweiten Spielers einer Menge M₂. So sind in den beiden Mengen gleiche Elemente enthalten. Diese Elemente bilden die "Schnittmenge" der beiden Mengen.

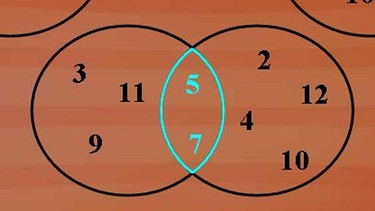
Die Zahlen 5 und 7 sind Elemente beider Mengen und bilden somit die Schnittmenge - klicken Sie bitte auf die Lupesomit die Schnittmenge

Die Menge M₁ besteht aus den Zahlen 3, 5, 7, 9 und 11, die Menge M₂ aus den Zahlen 2, 4, 5, 7, 10 und 12. So sind die Zahlen 5 und 7 Elemente beider Mengen und bilden somit die Schnittmenge M₁ geschnitten M₂.
Der nach unten geöffnete Halbbogen ist das Zeichen für "geschnitten mit".

Vereinigungsmenge

Vereinigungsmenge - klicken Sie bitte auf die Lupe

Sowohl die Menge M₁ der Karten des ersten Spielers als auch die Menge M₂ der Karten des zweiten Spielers wurden miteinander vermengt. Sie bilden jetzt die Vereinigungsmenge der beiden Mengen.

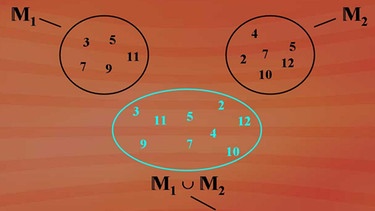
Unsere bekannten Mengen M₁ und M₂ werden in einer großen Menge vereint, welche die Elemente beider Mengen beinhaltet. Identische Elemente müssen nur einmal angegeben werden, in unserem Fall die 5 und die 7, und wir erhalten die Vereinigungsmenge M₁ vereinigt M₂.

Der nach oben geöffnete Halbbogen ist das Zeichen für vereinigt mit.