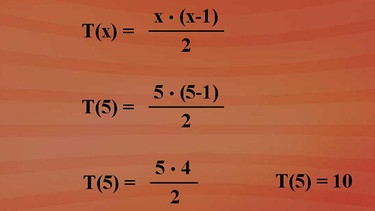Jährlich wird ein Wettkampf im Seilziehen ausgetragen. Es handelt sich dabei um acht bis zwanzig teilnehmende Teams.

Da die Anzahl der Teams erst kurz vor Veranstaltungsbeginn bekannt ist, wäre es schön, wenn man einen Term hätte, der uns sofort die Anzahl der Züge ermitteln lässt, wenn jedes Team gegen jedes andere Team ziehen soll.

Und einen solchen Term wollen wir jetzt aufstellen. Nehmen wir mal an, wir hätten nur drei Teams:

Drei Teams

Team 1 gegen Team 2, Team 1 gegen Team 3 und Team 2 gegen Team 3. Jede Verbindung zweier Teams entspricht einem Zug. Also drei Züge. Man könnte jetzt meinen, dass die Anzahl der Züge der Anzahl der Teams entspricht.

Vier Teams

Zum Test nehmen wir ein viertes Team dazu: 1 zieht gegen 2, 1 gegen 3, 1 gegen 4. 1 hat gegen alle gezogen, zwei gegen 1 schon eingetragen, 2 gegen 3, 2 gegen 4. So, jetzt hat auch Team 2 gegen alle gezogen. Team 3 muss noch gegen Team 4 ziehen. Somit sind alle untereinander verbunden. Es sind sechs Züge. Die Anzahl der Züge ist also nicht identisch mit der Anzahl der Teams.

Fünf Teams

Bei einem Team gibt es keinen Zug, bei zwei Teams Null plus 1 einen Zug. Bei drei Teams 1 plus 2 gleich drei Züge. Und bei vier Teams 1 plus 2 plus 3 gleich sechs Züge.

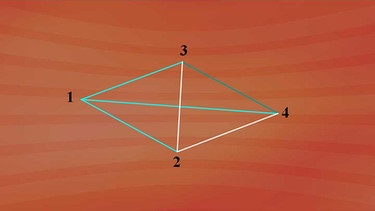
Dann wären das bei fünf Teams 1 plus 2 plus 3 plus 4 also zehn Züge. Das wollen wir nun grafisch überprüfen: Verbindet man bei fünf Teams jeden mit jedem, ergibt das zehn Verbindungslinien.

Einsatz einer Variablen

Wie sieht es jetzt aber aus, wenn wir für die Anzahl der Teams einen Platzhalter, sprich eine Variable setzen? Für die Anzahl der teilnehmenden Teams nehmen wir ein x. Bei x teilnehmenden Teams gibt es 1 plus 2 plus 3 plus 4 und so weiter bis plus x-1 in Klammern Züge. Als Termangabe: Term von x ist die gegebene Summe.

Einfachere Formel zur Berechnung der Züge

Von jedem Team x gehen (x -1) Verbindungslinien aus. Es gibt dann x mal (x-1) Verbindungen. Von jedem Punkt aus so betrachtet, haben wir aber jede mögliche Verbindung doppelt gezählt. Um das wieder zu regulieren, teilen wir unser Produkt durch 2.

Und wir erhalten den Term T von x ist x mal x-1 in Klammern geteilt durch 2.

Für fünf Teams waren es zehn Züge.

Termwert an der Stelle 5 ist gleich 5 mal Klammer auf 5 minus 1 Klammer zu geteilt durch 2.

Und somit 5 mal 4 geteilt durch 2 ist 20 geteilt durch 2 gleich 10.

Zusammenfassung

Wir haben einen Term aufgestellt, der uns für jede Belegung von x, sprich jede Teamanzahl, die Anzahl der Seilzüge sofort ermitteln lässt. Und nebenbei haben wir auch noch eine allgemein gültige Formel in der Mathematik aufgestellt.