GRIPS Mathe 31 Zuordnungen
1 kg Orangen kostet 1,80 €. Dem Kilogramm Orangen ist ein fester Preis zugeordnet. Um solche Zuordnungen geht es in dieser Lektion. Du erfährst, wie du Zuordnungen grafisch darstellen kannst und wie du sie berechnest.

Ordnet man etwas zu, legt man fest welche Dinge oder Begriffe zusammen gehören. In einem Geschäft ist zum Beispiel jeder Ware ein bestimmter Preis zugeordnet. Wenn du morgens deine Freunde mit dem Namen begrüßt hast du ihnen automatisch ihre Namen zugeordnet.
Auch in der Mathematik kommen Zuordnungen sehr häufig vor. Als Ausgangsgrößen hast du es meistens mit Zahlen zu tun, denen bestimmte Werte zugeordnet werden.
Darstellungsarten von Zuordnungen
Zuordnungen lassen sich auf verschiedene Art und Weise darstellen. Du kannst zum Beispiel ein Pfeilbild erstellen, eine Wertetabelle aufstellen oder ein Koordinatensystem zeichnen. Wir geben dir zu jeder Darstellungsart ein Beispiel:
Pfeilbild

An der Tankstelle siehst du, dass der aktuelle Preis von einem Liter Super bei 1,529 € liegt.
Nun kannst du jeder Menge (Literzahl) den entsprechenden Preis zuordnen:
2 Liter kosten demnach 3,058 € (2 · 1,529 €), 3 Liter 4,587 € (3 · 1529 €),
Liter 6,166 € (4 · 1,529 €) usw.
Wertetabellen

Wertetabellen werden verwendet, wenn es auf leichtes Ablesen ankommt. Beispiel: In einer Matheprobe waren 60 Punkte zu erreichen. In einem tabellarischen Notenschlüssel werden jeder Note bestimmte Punktwerte zugeordnet.
| Noten | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Punkte | 60 - 52 | 51 - 42 | 41 - 33 | 32 - 23 | 22 - 11 | 10 - 0 |
Koordinatensystem (Gitternetz)
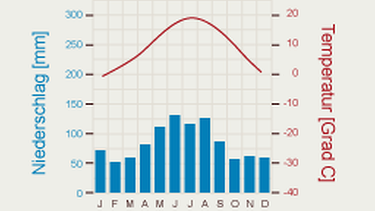
Hat man nur wenige Werte, so stellt man diese oft mit Säulen dar. Ein Beispiel dafür sind Klimadiagramme, die die durchschnittliche monatliche Niederschlagsmenge einer Stadt oder Region aufzeigen.
In diesem Diagramm sind die Niederschlagswerte der Stadt München im Verlauf der Monate dargestellt (blaue Säulen).
Bei der roten Temperaturkurve sind die einzelnen Werte miteinander verbunden. Diese Verbindungslinie wird als Graph bezeichnet.