GRIPS Mathe 31 Aufgaben zur linearen Funktion

In den beiden Aufgaben auf dieser Seite geht es um lineare Funktionen. Wir zeigen dir, wie du die Aufgaben graphisch löst beziehungsweise den Zweisatz oder den Dreisatz anwendest.
Graphische Lösung
Aufgabe 1
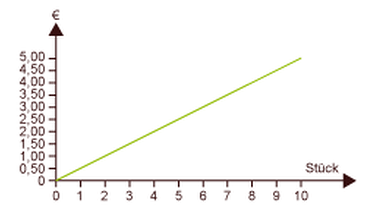
Wenn du alle Werte in eine Tabelle einträgst, weißt du sofort, wie teuer 1, 5 oder 10 Schokoriegel sind.
| Menge | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Preis | 0,50 | 1,00 | 1,50 | 2,00 | 2,50 | 3,00 | 3,50 | 4,00 | 4,50 | 5,00 |
Lösung mit dem Zweisatz
Ein Schaubild zu zeichnen und eine Wertetabelle zu erstellen, ist zehr zeitaufwändig, besonders wenn es sich um große Mengen handelt. Deutlich schneller, geht es mit einer einfachen Rechnung.
Aufgabe 2
Ein Schokoriegel kostet 0,50 €. Wie viel kosten 80 Stück?

Wie viel 80 Schokoriegel kosten, kannst du mit dem Zweisatz berechnen.
Antwort: Wenn 1 Schokoriegel 0,50 € kostet, dann kosten 80 Stück genau 80-mal so viel.
Zweisatz
Dieses Lösungsverfahren (diese Rechnung) wird als Zweisatz bezeichnet, da du in zwei Sätzen bzw. zwei Rechenschritten zu einer Lösung kommst:
Von der Einheit (1 Schokoriegel) zur Mehrheit (80 Schokoriegel).
Lösung mit dem Dreisatz
Wenn du den Grundpreis nicht kennst, also nicht weißt, was 1 Stück kostet, musst du noch einen Schritt einfügen.
Aufgabe 3
Für einen Ferienjob werden für 60 Arbeitsstunden 480 € angeboten. Du hättest Zeit, 40 Stunden zu arbeiten. Wie viel würdest du dann verdienen?
Um den Lohn für 40 Stunden berechnen zu können, musst du erst den Lohn für 1 Stunde berechnen.

Für 60 Stunden erhältst du 480 €. Demnach erhältst du für 1 Stunde genau den 60. Teil des Lohnes, also geteilt durch 60.
In 40 Stunden könntest du das
40-fache des Lohnes verdienen. Deshalb multiplizierst du im letzten Schritt den Lohn für 1 Stunde mal 40.
Antwort: Für 40 Stunden Arbeit würdest du 320 € erhalten.
Dreisatz
Dieses Lösungsverfahren heißt Dreisatz, da du in drei Schritten zu einer Lösung kommst: Von der Mehrheit (60 Stunden) über die Einheit (1 Stunde) zur neuen gesuchten Mehrheit (40 Stunden).