9. Quadratische Funktionen 9.4. Verschieben der Normalparabel
Bisher haben wir die Normalparabel nur in y-Achsenrichtung verschoben. Ob das wohl auch in x-Achsenrichtung funktioniert?
Um diese Frage zu untersuchen, wählen wir zur Normalparabel mit der Funktionsgleichung "y ist x2" wieder zwei weitere quadratische Funktionen, aber jetzt mit der Form
"y = (x - 1)2" und "y = (x + 2)2".
x-Intervalle für die Wertetabelle
Wertetabelle - klicken Sie bitte auf die Lupe
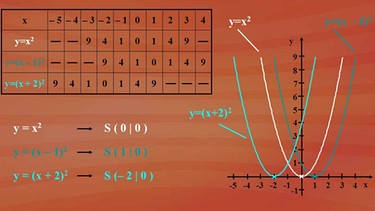
Um keine allzu großen y-Werte für die Zeichnung zu bekommen, wählen wir ganz bestimmte x-Intervalle für die Wertetabelle. Bei "y = x2" wählen wir den Bereich von -3 bis +3, für "y = (x - 1)2" den Bereich -2 bis +4 und für "(x + 2)2" das Intervall von -5 bis +1.
Setzen wir mal -2 in den Term "(x - 1)2" ein. Wir erhalten -2 - 1 = -3 und das zum Quadrat gibt 9.
die x-Koordinate des Scheitels
Nach diesem Muster berechnen sich auch die weiteren fehlenden Werte unserer Tabelle (siehe links), mit denen wir die gegebenen quadratischen Funktionen im Koordinatensystem grafisch darstellen können. Man kann in der Grafik erkennen, dass die x-Koordinate des Scheitels immer den Wert aufweist, dessen Belegung für x den Klammerwert 0 ergibt. Bei x - 1 zum Beispiel ist die Belegung für x = +1. Und bei x + 2 ist die Belegung für x = -2.
Fazit
Die Parabel mit der Funktionsgleichung "y = (x - 1)2" ist eine Normalparabel, deren Scheitel gegenüber der Normalparabel "y = x2" in x-Achsenrichtung um eine Einheit nach rechts verschoben ist. Für "(x + 2)2" erfolgt die Verschiebung in x-Achsenrichtung um zwei Einheiten nach links.
Allgemein gilt:
Klicken Sie btite auf die Lupe
Quadratische Funktionen der Form "y = (x - xs)2" sind nach oben geöffnete Normalparabeln mit den Scheitelkoordinaten xs und 0. xs ist deshalb als Variable gewählt, weil es die x-Koordinate des Scheitelpunktes ist.
Die Scheitelpunktform der Normalparabel
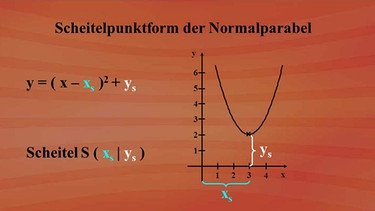
Scheitelpunktform der Normalparabel
Ist xs positiv, wird die Normalparabel "y = x2" in x-Achsenrichtung nach rechts verschoben. Ist xs negativ, geht das Ganze in die andere Richtung, also in x-Achsenrichtung nach links. Will man die in x-Achsenrichtung verschobene Normalparabel auch noch um ys in y-Achsenrichtung verändern, muss in der Funktionsgleichung ein Summand ys addiert werden. Die Funktionsgleichung einer in x-Achsen und y-Achsenrichtung verschobenen Normalparabel hat dann die Form "y = (x - xs)2 + ys". Am Graphen kann man sehen, dass der Scheitel der zu dieser Funktionsgleichung gehörenden Parabel die Koordinaten xs und ys hat. Man nennt diese Form einer quadratischen Funktion die Scheitelpunktform der Normalparabel. Der Name Scheitelpunktform kommt daher, weil die Koordinaten des Scheitels der Parabel direkt abgelesen werden können.