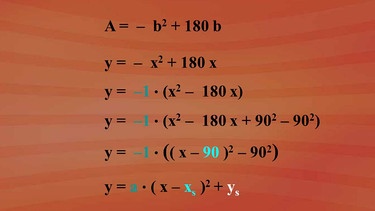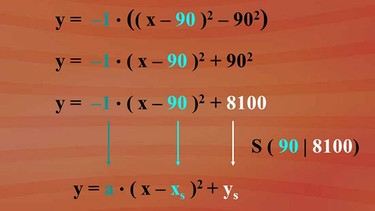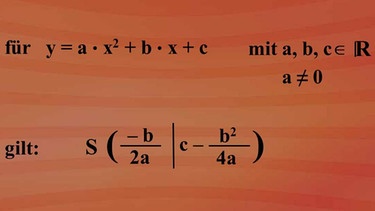9. Quadratische Funktionen 9.7. Beispiel zur allgemeinen Scheitelpunktform
Mit einem 360 Meter langen Zaun soll eine möglichst große Weidefläche abgesteckt werden. Da ist Rechnen angesagt - und die Anwendung der allgemeinen Scheitelpunktform.
In diesem Beispiel ist ein Extremwert gefragt. Das muss etwas mit einer quadratischen Funktion zu tun haben. Die Beiden haben uns schon sehr gut vorgerechnet, dass 360 Meter Zaun für zweimal Länge und zweimal Breite ausreichen müssen. Als Gleichung dargestellt:
2 · l für Länge + 2 · b für Breite = 360. Durch zwei geteilt, ergibt sich l + b = 180. Und nach l aufgelöst: l = 180 - b. Die Flächenmaßzahl A für ein Rechteck = Länge · Breite. Setzen wir für l den Term 180 - b ein, erhalten wir: A = (180 - b) · b, ausmultipliziert: -b2 + 180 b.
Das schaut nach einer quadratischen Funktion aus, Und das noch viel deutlicher, wenn man statt Flächenmaßzahl A ein y und statt Breite b ein x schreibt.
y = -x2 + 180 x.
Rekapitulation
Wir haben gelernt, dass man anhand der Scheitelform einer quadratischen Funktion direkt den Scheitel und somit den Extremwert ablesen kann. Und erinnern uns auch noch, dass für negative a-Werte ein maximaler Wert abgelesen werden kann, weil der Scheitel der höchste Punkt bei einer nach unten geöffneten Parabel ist. Wir müssen also versuchen, aus der Form
"y = -x2 + 180 x" eine Scheitelform zu bekommen.
Unser Ziel ist also eine Funktionsgleichung in der Form "y = a · (x - xs)2 + ys". Wenn wir -1 ausklammern, haben wir bereits einen Faktor a. Jetzt fehlt ein zweiter Binom, nämlich das (x - xs)2 .
In der dritten Folge hatten wir Binome besprochen, in der achten Folge haben wir Binome über quadratische Ergänzungen erhalten. Das wollen wir nun anwenden.
Anwendung der quadratischen Ergänzung
Die quadratische Ergänzung liefert uns - die Hälfte von 180 = 90 also - 902 - 902 .
Für x2 - 180 x + 902 können wir in der Quadratschreibweise (x - 90)2 setzen und -902 wird abgeschrieben. Mit -1 ausmultipliziert, ergibt sich -1 · (x - 90)2 + 902 . Und wir haben die Scheitelform y = -1 · (x -90)2 + 8100 mit dem Scheitel S 90 und 8100.
Was sagt diese Scheitelform aus?
Es ist eine nach unten geöffnete Normalparabel, da a = -1. Der höchste Funktionswert ist 8100 für x = 90. x haben wir für die Breite b gewählt und y für die Flächenzahl A.
Somit ist der maximale Flächeninhalt, den man erreichen kann, 8100 Quadratmeter - wenn als Breite 90 Meter gewählt wird. Zur Vervollständigung berechnen wir noch die Länge: Sie beträgt 360 Meter minus 2 · 90 Meter für die beiden Breiten, geteilt durch zwei. Also auch 90 Meter.
Bitte merken!:
Das flächengrößte Rechteck ist bei gleichem Umfang immer das Quadrat.
Berechnung mittels Formel
Im Beispiel haben wir aus der allgemeinen Form einer quadratischen Funktion die Scheitelform hergeleitet. Aber man kann auch die Scheitelkoordinaten über eine Formel, die im Begleitmaterial erläutert wird, aus der allgemeinen Form der quadratischen Funktion direkt ermitteln. Man erspart sich dann die mühseligen und fehlerbehafteten Umformungen über quadratische Ergänzung. Die Formel steht in der Formelsammlung.
Sie lautet:
Für die allgemeine Form "y = a · x2 + b · x + c" ist die x-Koordinate des Scheitelpunktes -b : 2a und die y-Koordinate des Scheitels c - b2 : 4a.
Mit dieser Formel hätten wir unsere Weidezaun-Aufgabe schneller gelöst: "y = -1 · x2 + 180 · x + 0" war unsere Ausgangsfunktion. Nun wird a, b und c zugeordnet. Das Ergebnis der Grafik: 90 und 8100.