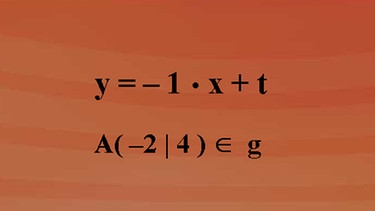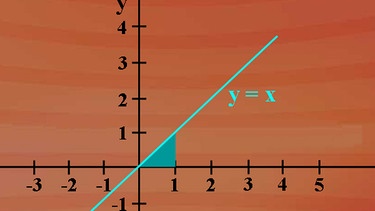Jetzt wollen wir noch die Geradengleichung ermitteln, wenn zwei Punkte gegeben sind.

Beispiel

Wählen wir die Punkte A mit minus zwei und vier und B mit drei und minus eins - grafisch ermittelt durch das Einzeichnen von A und B.

Den Steigungsfaktor können wir über das Steigungsdreieck schnell berechnen. Der Steigungsfaktor m ist ja Δy durch Δx. Also im Zähler die Differenz der y-Koordinaten zweier Punkte und im Nenner die Differenz der x-Koordinaten dieser beiden Punkte.

Sie müssen nur darauf achten, dass Sie immer als Minuend die Koordinaten des gleichen Punktes verwenden. Natürlich gilt das auch für den Subtrahend. Weiter in unserem Beispiel:

m ist im Zähler minus eins für die y-Koordinate des Punktes B, minus vier für die y-Koordinate des Punktes A - im Nenner entsprechend für die x-Koordinaten. Der Zähler zusammengefasst ergibt minus fünf und der Nenner fünf. Der Steigungsfaktor der Geraden durch die Punkte A und B ist demnach minus eins.

Nun wissen Sie, wie man die Steigung einer Geraden bestimmt, wenn zwei Punkte gegeben sind. Jetzt fehlt uns nur noch der y- Achsenabschnitt t, um die Funktionsgleichung in der Normalform angeben zu können. Aber das ist nicht mehr schwierig. Denn wir haben ja zwei Punkte, die auf der Geraden liegen.

Beispiel - klicken Sie bitte auf die Lupe

Bis jetzt hat die Funktionsgleichung die Form "y ist gleich minus eins für m mal x plus t". Da wir den Punkt A als Element der Geraden kennen, müssen die Koordinatenwerte von A in die Funktionsgleichung eingesetzt eine wahre Aussage ergeben und somit die Berechnung von t ermöglichen.

Wir erhalten vier für y gleich minus eins mal minus zwei für x plus t. Und das führt zu dem Ergebnis t gleich zwei. Die Funktionsgleichung der Geraden in der Normalform lautet: "y ist gleich minus eins mal x plus zwei".

Besondere Geraden: Beispiel 1

Beispiel 1

Nun noch Beispiele für besondere Geraden: Als erstes Beispiel betrachten wir die Gerade mit der Funktionsgleichung y = x.

Es ist eine Ursprungsgerade mit der Steigung eins durch eins. Diese Gerade bildet die Winkelhalbierende des I. und III. Quadranten unseres Koordinatensystems.

Besondere Geraden: Beispiel 2

Beispiel 2

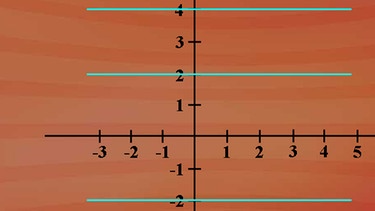
Als zweites Beispiel betrachten wir Geraden mit der Gleichung "y = t". Es handelt sich um Geraden mit der Steigung m gleich Null. Für jede Belegung von t erhält man parallele Geraden zur x-Achse durch den Punkt 0 und t auf der y-Achse. Die linearen Funktionsgleichungen sind konstante Funktionen.

Besondere Geraden: Beispiel 3

Beispiel 3

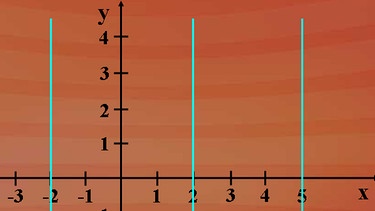
Als drittes Beispiel betrachten wir noch Geraden, die parallel zur y-Achse verlaufen. Alle Punkte einer solchen Geraden haben bei unterschiedlichen y-Werten den gleichen x-Wert, wie zum Beispiel auf der Geraden mit der Geradengleichung "x = 2". Aber hier aufgepasst: Die Geraden sind nicht Graphen von Funktionen, sondern nur von Relationen!

Bei einer Funktion darf jedem x-Wert nur ein y-Wert zugeordnet sein!