Eine 5 cm hohe brennende Kerze steht 7 cm vor einem Hohlspiegel mit dem Krümmungsradius r = 8 cm. Welche Aussagen kann man über das Bild der Kerze machen? Führe die entsprechende Bildkonstruktion durch und berechne die Bildweite b und -größe B.

Aus dem Krümmungradius r = 8 cm des Spiegels ergibt sich dessen Brennweite f, sie ist halb so groß wie r, das heißt es gilt: f = 4 cm. Da der Gegenstand zwischen dem Krümmungsmittelpunkt und dem Brennpunkt steht, entsteht ein reelles, vergrößertes, umgekehrtes und seitenverkehrtes Bild der Kerze. Zur Bildkonstruktion verwendet man 2 der 3 ausgezeichneten Strahlen, von denen man den Verlauf nach der Reflexion am Spiegel kennt, zum Beispiel den Parallel- und den Brennpunktstrahl. Nach der Reflexion vertauschen sie ihre Rollen:

Berechnung der Bildweite b und der Bildgröße B: Für die Abbildung am Hohlspiegel gelten dieselben Beziehungen wie bei der Abbildung durch eine Sammellinse:
(1) 1/g + 1/b = 1/f
und
(2) B/G = b/g   

Die Übereinstimmung hat ihre Ursache darin, dass die abbildenden Flächen sowohl beim Hohlspiegel als auch bei der Sammellinse kugelschalenförmig sind.

(1) aufgelöst nach 1/b ergibt: 1/b = 1/f – 1/g bzw. die rechte Seite auf gemeinsamen Nenner:     
1/b = (g – f)/f · g
Durch Kehrwertbildung ergibt sich daraus die Bildweite b, das heißt der Abstand des Bildes von der Linse: 
b = f · g/(g – f)
b = 4 cm · 7 cm / (7 cm – 4 cm) = 9,3 cm

Die Bildweite b beträgt 9,3 cm. Das Bild liegt also hinter dem Krümmungsmittelpunkt des Spiegels.

Für die Bildgröße folgt aus (2): B/G = b/g durch Auflösen nach B:
B = b · G/g
B = 9,3 cm · 5 cm/7 cm = 6,7 cm

Das heißt: Das Bild ist – wie auch die Konstruktion zeigt – vergrößert.

Wie ändert sich das Bild, wenn die Kerzenflamme zum Spiegel hin verschoben wird?

Das Bild bleibt zunächst reell, kann also auf einem Schirm "aufgefangen" werden. Es ist nach wie vor umgekehrt, wird immer größer und entfernt sich immer weiter vom Spiegel. Wenn die Kerzenflamme in der Brennebene des Spiegels steht, verschwindet das Bild, um bei weiterer Annäherung an den Spiegel als virtuelles, aufrechtes und vergrößertes Bild, das hinter dem Spiegel liegt und das man nur sehen kann, wenn man in den Spiegel blickt, wieder zu erscheinen.

Die 5 cm große Kerze aus der vorigen Aufgabe wird nun 10 cm entfernt von einem Wölbspiegel mit demselben Krümmungsradius von 8 cm aufgestellt. Ermittle das Bild der Kerze zeichnerisch und überprüfe deine Lösung durch Rechnung! 
Erscheint das Bild vergrößert oder verkleinert?                                                                                                    

Beim Wölbspiegel liegt der (hier virtuelle) Brennpunkt genau zwischen dem Krümmungsmittelpunkt und dem Spiegel. Die Brennweite (beim Wölbspiegel negativ wegen der konvexen Krümmung) ist daher ebenfalls halb so groß wie der Krümmungsradius. Für die Bildkonstruktion eignen sich dieselben Strahlen wie beim Hohlspiegel: Parallelstrahl und Brennpunktstrahl, wobei der Parallelstrahl am Spiegel so reflektiert wird, als wenn er scheinbar vom Brennpunkt her käme. Der Brennpunktstrahl ist von der Kerzenflamme auf den Brennpunkt gerichtet und wird als Parallelstrahl reflektiert.

Berechnung: Bei der Bestimmung der Bildweite und -größe muss man beachten, dass es sich beim Wölbspiegel um einen virtuellen Brennpunkt handelt und die Brennweite daher negativ ist: f = - 4 cm
Mit b = f · g/(g – f) ergibt sich:
b = - 4 cm · 10 cm/[10 cm – (- 4 cm)] = - 40 cm² / 14 cm = - 2,9 cm
Das Minus-Zeichen besagt, dass es sich um ein virtuelles Bild handelt, das hinter dem Spiegel zu sehen ist.

Für die Größe des Bildes ergibt sich mit B = -b · G / g
B = 2,9 cm · 5 cm / 10 cm = 1,4 cm

Die Kerze ist 5 cm groß, das Bild nur 1,4 cm. Es ist demnach verkleinert.

Rückspiegel im Auto haben eine konvexe Spiegelfläche, sind also Wölbspiegel.

Konvexspiegel verhelfen zu einem größeren Gesichtsfeld, das heißt man erkennt einen größeren Bereich als in einem ebenen Spiegel. Daher werden Wölbspiegel auch als Verkehrsspiegel an unübersichtlichen Straßeneinmündungen aufgestellt.
Da das im Rückspiegel sichtbare virtuelle Bild eines hinterher fahrenden Autos verkleinert ist, entsteht der Eindruck, dass das Auto weiter entfernt ist als dies im Wirklichkeit der Fall ist.

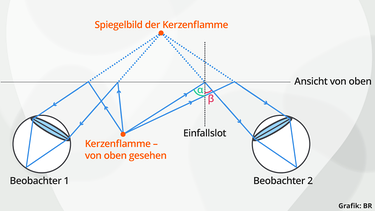
Erkläre anhand einer Zeichnung, warum das Spiegelbild, das ein ebener Spiegel zum Beispiel von einer brennenden Kerze erzeugt, von überall her an derselben Stelle erscheint.