10. Schnittmengen von Funktionen 10.2. Schnittpunkt-Bestimmung
In dieser Folge beschäftigen wir uns mit der Schnittpunkt-Bestimmung zwischen Geraden und Geraden, Parabeln und Parabeln sowie Geraden und Parabeln. Beginnen wir mit dem Schnittpunkt zweier Geraden. Dazu benötigen wir erst einmal zwei Geradengleichungen.
Stellen Sie sich vor, Sie möchten beim Sägewerk Bauholz kaufen. Hätten Sie gedacht, dass es da hilfreich ist, über die Schnittpunkt-Bestimmung von zwei Geraden Bescheid zu wissen? Im Folgenden erfahren Sie, warum das so ist.
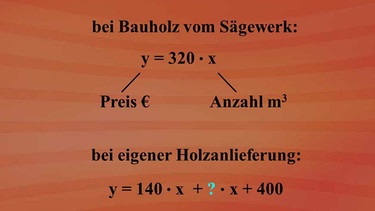
Es wurden zwei Möglichkeiten für den Kauf des Bauholzes angeboten, beide Formel finden Sie in der nebenstehenden Grafik und im Popup. Bei selbst angeliefertem Rundholz wurden eine Grundpauschale und die Schnittkosten für das Bauholz fällig. Wenn der Kunde das Rundholz vom Sägewerk bezieht, waren im Beispiel 320 Euro pro Kubikmeter Bauholz zu bezahlen.
Erste Möglichkeit
Die beiden Möglichkeiten wollen wir uns in linearen Funktionen dargestellt vorstellen. Nehmen wir zuerst die einfachere Variante, bei der alles vom Sägewerk bezogen wird. Die Variable y soll der zu bezahlende Preis sein, die Variable x die Anzahl der Kubikmeter. Der Bauholzpreis beträgt pro Kubikmeter 320 Euro. Dann ist der Preis für den direkten Ankauf vom Sägewerk: "y = 320 · x" (siehe Grafik).
Zweite Möglichkeit
Die Variablenbelegung von x und y wird beibehalten. y bleibt also der zu bezahlende Betrag und x die Anzahl der Kubikmeter Bauholz. Aber wir wissen noch nicht, wie viel ein Kubikmeter Holz im Ankauf kostet. Wir wissen nur: Es ist eine Pauschale von 400 Euro zu zahlen, und das Schneiden kostet 140 Euro pro Kubikmeter. Dies als Funktionsgleichung: "y = 140 · x (für die Schnittkosten) + Fragezeichen · x (für die Holzkosten) + 400 (für die Pauschale)" (siehe Popup).
Schauen wir nochmals zum Sägewerk:
Was hat der Sägewerksbesitzer gerechnet? Hatte er eine Tabelle? Oder ein anderes Hilfsmittel? Unsere Funktionsgleichung für die zweite Möglichkeit können wir auf alle Fälle vervollständigen: "y = 140 · x + ..." Für das Fragezeichen setzen wir die 80 Euro für den Holzpreis ein und erhalten "... 80 · x + 400". Die x-Glieder zusammengefasst: "y = 220 · x + 400". Die Funktionsgleichung ist auch im Grafik-Popup sichtbar.
Grafische Darstellung
Die beiden Funktionsgleichungen sind Geradengleichungen, die wir in einem geeigneten Koordinatensystem darstellen können.
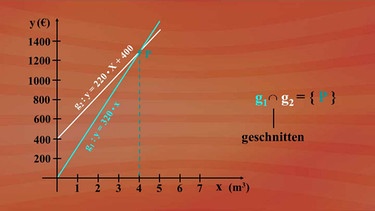
Die erste Möglichkeit - wenn alles vom Sägewerk bezogen wird - stellen wir mit der Geraden 1 dar, die zweite Möglichkeit mit der Geraden 2.
Der Verlauf der beiden Geraden zeigt, dass bei einem Ankauf von vier Kubikmetern Holz bei beiden Möglichkeiten der gleiche Preis zu zahlen ist. Unter vier Kubikmetern ist der Ankauf vom Sägewerk die günstigere Variante, über vier Kubikmeter führt das Anliefern des eigenen Holzes zu einem Preisvorteil.
Der wichtigste Punkt ist also der Schnittpunkt der beiden Geraden. Er bildet die Schnittmenge.