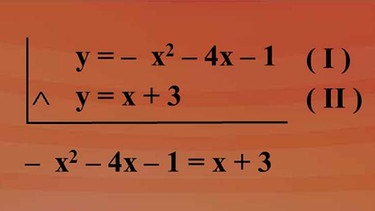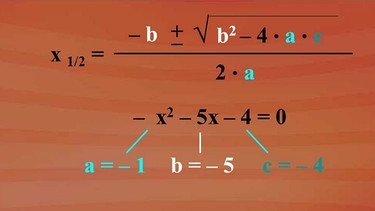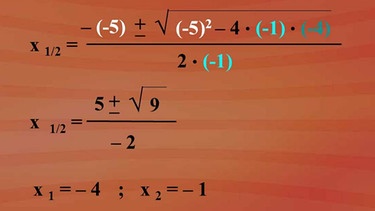Wählen wir als Beispiel die Parabel p mit der Gleichung "y = -x² - 4x - 1" und die Gerade g: "y = x + 3". Die nebenstehende grafische Darstellung zeigt, dass Parabel und Gerade zwei gemeinsame Punkte haben - nennen wir sie P₁ und P₂. p geschnitten g ist somit die Menge der Punkte P₁ und P₂.

Ziel: Gleichung mit einer Variablen

So erhält man eine Gleichung mit nur noch einer Variablen - klicken Sie bitte auf die Lupe

Wie bei der Schnittpunktbestimmung zweier Geraden fasst man die beiden Gleichungen zu einem Gleichungssystem zusammen und erhält das System mit den Gleichungen, das auch in der Grafik dargestellt ist: "y = -x² - 4x - 1" als Gleichung I und "y = x + 3" als Gleichung II. Mit dem Gleichsetzverfahren kommen wir auf eine Gleichung mit nur noch einer Variablen.

Lösung mittels Formel

Lösung mittels Formel - klicken Sie bitte auf die Lupe

Gleichungen mit einer Variablen können wir lösen. Zwar tritt die Variable ein Mal mit der Hochzahl zwei auf, aber auch das ist nichts Neues mehr. Es ist eben eine quadratische Gleichung, für die wir zur Lösung eine Formel in unserer Formelsammlung haben. Und da steht: Die Gleichung "ax² + bx + c = 0", hat die Lösungen "x_1/2" ist gleich im Zähler "-b + oder - Wurzel aus b² - 4ac" und im Nenner "2a". Den Ansatz finden Sie in der Grafik.

Umformung der Ausgangsgleichung

Umformung der Ausgangsgleichung - klicken Sie bitte auf die Lupe

Wenn man solch eine Formel hat, muss man die Ausgangsgleichung so umformen, dass die zur Anwendung nötige Form dasteht. Und das werden wir jetzt tun.

Zuerst stellen wir die Form "= 0" her, indem wir x + 3 auf die linke Gleichungsseite bringen. Es ergibt sich wie dargestellt: "-x² - 5x - 4 = 0". a, b, c für die Formel können abgelesen und eingesetzt werden.

Wenn man bei den vielen Minuszeichen keine Fehler macht, führt die Berechnung über "x_1/2 = 5 +/- Wurzel aus 9 geteilt durch -2" zu den beiden Ergebnissen "x₁ = -4" und "x₂ = -1" (siehe Bild).