10. Schnittmengen von Funktionen 10.5. Schnittpunkt mittels Geradengleichung
Man kann den Schnittpunkt über die Parabelgleichung oder die Geradengleichung ermitteln. Wir führen hier die Variante mit der Geradengleichung vor - sie ist die einfachere.
Die x-Werte der beiden Schnittpunkte sind nun bekannt. Da wir wissen, dass die beiden Schnittpunkte gemeinsame Punkte von Gerade und Parabel sind, ist es jedem selbst überlassen, ob er die dazugehörigen y-Werte über die Parabelgleichung oder die Geradengleichung ermittelt. Die einfachere Variante ist sicher die Geradengleichung:
Algebraische Darstellung
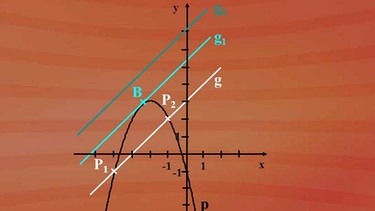
"x1 = -4" in g wie dargestellt eingesetzt führt zum y-Wert -1 und somit zum Punkt P1 mit den Koordinaten -4 und -1.
"x2 = -1" in g eingesetzt, liefert den y-Wert 2 für den Punkt P2.
Die PunkteP1 und P2. sind die Lösungselemente unseres Gleichungssystems. Diese Lösungsmenge ist die Schnittmenge der Lösungsmengen der beiden Funktionsgleichungen:
p geschnitten g ist die Menge der Punkte -4, -1 (für P1 ) und -1, 2 (für P2.). In der Lösungsmenge geschrieben sieht das so aus, wie in der nebenstehenden Grafik dargestellt.
Grafische Darstellung
Grafische Darstellung - klicken Sie bitte auf die Lupe
Aber haben Geraden mit Parabeln immer zwei Schnittpunkte? Betrachten Sie dazu das nebenstehende Bild. Wir behalten die Steigung der Geraden g bei und ändern den y-Achsenabschnitt, beliebig viele Geraden könnten somit eingezeichnet werden. Wir beschränken uns auf jedoch zwei besondere Geraden: Die Gerade g1 besitzt nur einen gemeinsamen Punkt mit der Parabel, den Berührpunkt B. Die Gerade g0 hat dagegen überhaupt keinen gemeinsamen Punkt mit der Parabel.
Die Diskriminante
Die Frage ist nun, ob man auch mit der Berechnung erkennen kann, ob es zwei Schnittpunkte, einen Berührpunkt oder keinen gemeinsamen Punkt gibt. Erinnern sie sich noch an die Lösung von quadratischen Gleichungen?
Wenn in der Lösungsformel unter der Wurzel ein negativer Wert stand, gab es kein Lösungselement, stand unter der Wurzel der Wert 0, gab es genau ein Lösungselement, war der Wert unter der Wurzel positiv, gab es zwei Lösungselemente.
Die Diskriminante
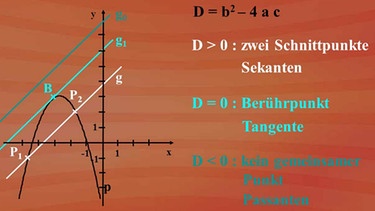
Da der Wert unter dem Wurzelzeichen darüber entscheidet, wie viele Lösungselemente es gibt, nennt man den Term nach den lateinischen Wort "discriminare" für "unterscheiden" die Diskriminante, sie ist nebenstehend dargestellt.
"b2 - 4ac" heißt Diskriminante D. Für D > 0 erhalten wir zwei Schnittpunkte, für D = 0 einen gemeinsamen Punkt, den Berührpunkt. Für D < 0 gibt es keinen gemeinsamen Punkt.
Zusammenfassung
Zusammenfassung - klicken Sie bitte auf die Lupe
Man kann auch sagen: Für D > 0 ergeben sich Sekanten, für D = 0 eine Tangente und für D < 0 Passanten. Alles nach lateinischen Wörtern bezeichnet: "secare" heißt schneiden, "tangere" berühren und "passare" vorbeigehen. Sie finden die Zusammenfassung auch in der Grafik.