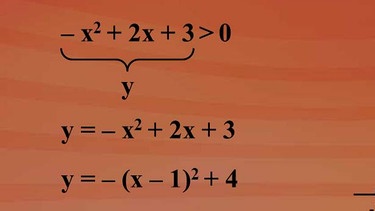Analog zu den quadratischen Gleichungen haben quadratische Ungleichungen die nebenstehende allgemeine Form. Dem Term "ax² + bx + c" weisen wir die Termwerte y zu. Jetzt haben wir die Möglichkeit, die Termwerte grafisch darzustellen.

Ein einfaches Beispiel

Ein einfaches Beispiel

Wählen wir die nebenstehende Ungleichung. Die Termwerte sind y. Es ergibt sich mit "y = -x² + 2x + 3" eine Parabelfunktion. Über die Scheitelpunkt-Bestimmung oder die quadratische Ergänzung ergibt sich die Scheitelform - (siehe nebenstehendes Bild) schon kann man den dazugehörigen Grafen zeichnen:

Grafische Darstellung

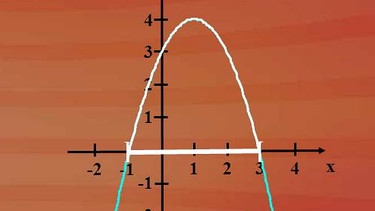
Wir haben den Term, für den untersucht werden soll, bei welcher Belegung von x Termwerte > 0 entstehen, grafisch dargestellt - bitte klicken Sie nebenstehende Grafik an. Die Schnittpunkte mit der x-Achse zeigen uns die Werte, für die der Term Null annimmt, es sind die Nullstellen der Funktion.

Uns interessiert aber, für welche Belegungen von x ein Termwert > 0 entsteht. Das kann man am Graphen direkt ablesen: Unterhalb der x-Achse liegen die Termwerte, die < 0 sind, oberhalb der x-Achse liegen die Termwerte, die > 0 sind.

Wichtig: die Nullstellen

Am wichtigsten sind also die Nullstellen selber, da diese die Grenzen angeben. Die Nullstellen werden über die Lösungsformel für quadratische Gleichungen bestimmt. Für unser Beispiel sind es die x-Belegungen -1 und 3.

Betrachten Sie noch einmal die Grafik: Der Parabelbogen oberhalb der x-Achse zeigt die Termwerte größer als Null. Sie ergeben sich aus x-Belegungen zwischen -1 und 3, wobei die Grenzen nicht dazugehören - denn dann wäre y = 0.

Die Lösungsmenge

Somit können wir die Lösungsmenge angeben. L ist die Menge der Belegungen von x mit der Eigenschaft, dass x > als -1 und < 3 sein muss. Oder in der Intervallschreibweise: L ist das Intervall von -1 bis 3, wobei die Grenzen ausgeschlossen sind. Das ist ersichtlich durch die abgewandten Klammern.